In an earlier post, we have seen how to add a new node to a binary tree.
Normally when we talk about binary tree, we refer to binary search tree which is ordered tree.
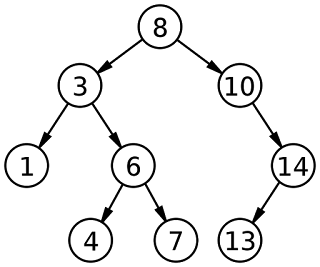
Let us write the inorder for the BST given above.
In inorder, we start with root 8. But before we visit 8, we should visit all nodes of left subtree. So we branch to 3. Before we visit 3, we go to its left child 1. Since 1 has no left child, we print 1. Now we have visited complete left branch of 3. So we print 3 and then we go to 6. Before we print 6, we should go to its left child 4. As 4 is leaf node (node with no children), it is printed. After visiting 4, which is left branch of 6, we can print parent viz 6. Next we go to right branch of 6.
So you can write down like this.
But a recursive function for these in very simple. Or really very small.
Binary Tree Terminology:
- Tree is a non-linear data structure where every node has multiple branches
- A binary tree is a tree where each node has maximum 2 branches
- Each node branching out is called child node
- The starting node of the tree is called root
- The two children of binary tree are left child and right child.
- The child node along with its branches and sub-branches are called sub-tree.
- A node has two sub-trees - left subtree and right subtree
- A node which has no child nodes and hence no subtrees is called a leaf node

Image from : http://msoe.us/taylor
Normally when we talk about binary tree, we refer to binary search tree which is ordered tree.
In a binary search tree, every node to the right of a given node will have larger value than the given node. And every node to the left of given node will have value smaller than given node.
That is to say the left subtree of any node has values smaller than parent and right subtree of any node has values larger than parent. Tree traversal
In case of lists, stacks or queues, the traversal was simple. Because they are linear data structures. You start from first node, then visit the second node, then third node and so on until last node. Or you can start from last node and come backwards till first node.
But a tree is a non-linear structure. Each node has multiple branches. In case of binary tree, each node has two branches (also called children)- left and right. So which node to we visit after a given node? Its left child ? Or its right child? How do we ensure that we visit all the nodes of the tree and visit these nodes only once?
There are three ways of traversing a tree.
- In order traversal - For any node,
- we visit all the nodes in left subtree of a node,
- visit parent,
- visit all nodes in right subtree
- Pre order traversal -
- We visit the parent node
- visit all nodes of left subtree
- visit all nodes of right subtree.
- Post order traversal -
- We visit visit all nodes of left subtree
- visit all nodes of right subtree
- and finally we visit parent node.
Let us write the inorder for the BST given above.
- Inorder - 1 -- 3 -- 4 -- 6 -- 7 -- 8 -- 10 -- 13 -- 14
- Preorder 8 -- 3 -- 1 -- 6 -- 4 -- 7 -- 10 -- 14 -- 13
- Postorder 1 -- 4 -- 7 -- 6 -- 3 -- 13 -- 14 -- 10 -- 8
In inorder, we start with root 8. But before we visit 8, we should visit all nodes of left subtree. So we branch to 3. Before we visit 3, we go to its left child 1. Since 1 has no left child, we print 1. Now we have visited complete left branch of 3. So we print 3 and then we go to 6. Before we print 6, we should go to its left child 4. As 4 is leaf node (node with no children), it is printed. After visiting 4, which is left branch of 6, we can print parent viz 6. Next we go to right branch of 6.
So you can write down like this.
But a recursive function for these in very simple. Or really very small.
void in_order(NODEPTR nd) { if(nd!=NULL) { in_order(nd->left);/*visit left subtree*/ printf("%d---",nd->val); in_order(nd->right);/*visit right subtree*/ } }
When you run the program, you will notice that, inorder traversal will print the nodes in ascending order of values.
Similarly you can write preorder and postorder traversal functions too.
void pre_order(NODEPTR nd) { if(nd!=NULL) { printf("%d---",nd->val); pre_order(nd->left); pre_order(nd->right); } } void post_order(NODEPTR nd) { if(nd!=NULL) { post_order(nd->left); post_order(nd->right); printf("%d---",nd->val); } }
Here is the complete program.
#include<stdio.h> #include<stdlib.h> struct node { int val; struct node *left; struct node *right; }; typedef struct node *NODEPTR; NODEPTR create_node(int num) { NODEPTR temp = (NODEPTR)malloc(sizeof(struct node)); temp->val = num; temp->left = NULL; temp->right = NULL; return temp; } NODEPTR insert_node(NODEPTR nd,NODEPTR newnode) { if(nd==NULL) return newnode;/* newnode becomes root of tree*/ if(newnode->val > nd->val) nd->right = insert_node(nd->right,newnode); else if(newnode->val < nd->val) nd->left = insert_node(nd->left,newnode); return nd; } void in_order(NODEPTR nd) { if(nd!=NULL) { in_order(nd->left); printf("%d---",nd->val); in_order(nd->right); } } void pre_order(NODEPTR nd) { if(nd!=NULL) { printf("%d---",nd->val); pre_order(nd->left); pre_order(nd->right); } } void post_order(NODEPTR nd) { if(nd!=NULL) { post_order(nd->left); post_order(nd->right); printf("%d---",nd->val); } } int main() { NODEPTR root=NULL; int n; do { NODEPTR newnode; printf("Enter value of node(-1 to exit):"); scanf("%d",&n); if(n!=-1) { newnode = create_node(n); root = insert_node(root,newnode); } } while (n!=-1); printf("Preorder traversal\n"); pre_order(root); printf("\nInorder traversal\n"); in_order(root); printf("\nPostorder traversal\n"); post_order(root); return 0; }
Comments
Post a Comment