Skip to main content

Doubly Linked List

Doubly Linked List is a list where each node has two links - one to the next node and another to the previous node.


Because of two links, operations on this list are considerably easier. But there is an overhead of one more pointer in each node.

First we need to have a node for the list. As I mentioned earlier, the node will have data - in this case a simple integer and two pointers.



 struct node  
 {  
   int n;  
   struct node *next;  
   struct node *prev;  
 };  
 typedef struct node * NODEPTR;

We have typedefined NODEPTR as we will be use it often.

Next we have to define two pointers - head of the list and tail of the list. And let us not forget to initialize them to NULL.


 int main()  
 {  
          NODEPTR head,tail;      
          head = tail = NULL;

Our create_node function will be similar to that of singly linked list. Only difference is we have to initialize newnode->prev as well. To NULL.

Let us write functions to insert a node to  list. Let us see two simple cases 
  • insert the node at the beginning of the list 
  • and append the node at the end of the list.

Insert node to DLL

 



As can be seen from the diagram, we should link the new node before the head node. 
  1. We just need to set head->prev to newnode 
  2. and newnode->next to head.
  3. And then set newnode to be head
But this will give us a problem when the list is empty viz head is null. head->prev gives segmentation fault. 

To avoid that we have to make a slight adjustment in our first step
  1. If head is not NULL set head->prev to newnode 
Now we are ready to write our insert_node function. Here is the function


 NODEPTR insert_node(NODEPTR head, NODEPTR newnode)  
 {  
    newnode->next = head;  
    if(head)  
    {  
      head->prev = newnode;  
    }  
    head = newnode;  
    return head;  
 }

Append node to DLL

 

Here we should add the new node to the end of DLL. So, we have to modify tail. 
  1. Set tail->next to newnode
  2. Set newnode->prev to tail
  3. Define newnode as tail
Again there will be a problem when tail is NULL. That is when the list is empty. So change our first step to
  1. Set tail->next to newnode if tail is not NULL


 NODEPTR append_node(NODEPTR tail, NODEPTR newnode)  
 {  
    if(tail!=NULL)//only if the list is non-empty
      tail->next = newnode;  
    newnode->prev = tail;  
    tail = newnode;  
    return tail;  
 }

DLL traversal  

 

Traversal of DLL is similar to that of SLL. But we can also traverse the nodes in reverse order, starting from last node.

void display_nodes_reverse(NODEPTR tail)  
 {  
   NODEPTR temp = tail;//redundant!
   while (temp!= NULL)  
   {  
     printf("%d====>",temp->n);  
     temp = temp->prev;  
   }  
 }

Here is our complete program 

#include<stdio.h>  
#include<stdlib.h>
 struct node  
 {  
   int n;  
   struct node *next;  
   struct node *prev;  
 };  
 typedef struct node * NODEPTR;  
 NODEPTR create_node(int value);  
 NODEPTR insert_node(NODEPTR head,NODEPTR newnode);  
 NODEPTR append_node(NODEPTR tail, NODEPTR newnode);  
 void display_nodes(NODEPTR head);  
 void display_nodes_reverse(NODEPTR tail); 

 NODEPTR create_node(int value)  
 {  
   NODEPTR temp = (NODEPTR) malloc(sizeof(struct node));  
   temp->prev = temp->next = NULL;  
   temp->n = value;  
   return temp;  
 } 

 NODEPTR insert_before_head(NODEPTR head, NODEPTR newnode)  
 {  
    newnode->next = head;  
    if(head)  
    {  
      head->prev = newnode;  
    }  
    head = newnode;  
    return head;  
 } 

 NODEPTR append_node(NODEPTR tail, NODEPTR newnode)  
 {  
    if(tail!=NULL)
     tail->next = newnode;  
    newnode->prev = tail;  
    tail = newnode;  
    return tail;  
 } 

void insert_after( NODEPTR*tailptr,NODEPTR newnode,NODEPTR n1)
{
        //add the node after n1
        NODEPTR n2 = n1->next;
        n1->next = newnode;
        newnode->prev = n1;
        newnode->next = n2;
        if (n2!=NULL)//if n1 is not the last node
        {
          n2->prev = newnode;
        }
        if(n1==(*tailptr))
        {
            *tailptr =  newnode;//adding after last node. Make newnode as tail
        }
} 

 void display_nodes(NODEPTR head)  
 {  
   NODEPTR temp = head;//redundant 
   while (temp!= NULL)  
   {  
     printf("%d====>",temp->n);  
     temp = temp->next;  
   }  
 } 

 void display_nodes_reverse(NODEPTR tail)  
 {  
   NODEPTR temp = tail;//redundant 
   while (temp!= NULL)  
   {  
     printf("%d====>",temp->n);  
     temp = temp->prev;  
   }  
 } 

 int main()  
 {  
     NODEPTR head,tail;  
     NODEPTR newnode;  
     int numnodes,i;  
     //initialize head and tail. Very important!!  
     head = tail = NULL;  
     printf("Number of nodes = ");  
     scanf("%d",&numnodes);  
     
     for(i = 0;i<numnodes/2;i++)  
     {  
       int value;  
       NODEPTR newnode;  
       printf("node value=");  
       scanf("%d",&value);  
       newnode = create_node(value);  
       tail = append_node(tail,newnode);
       if(head==NULL)  
       {  
          head = tail;  
       }  
     }  
     for( ;i<numnodes;i++)  
     {  
       int value;  
       NODEPTR newnode;  
       printf("node value=");  
       scanf("%d",&value);  
       newnode = create_node(value);  
       head = insert_before_head(head,newnode);
       if(tail==NULL)  
       {  
          tail = head;
       }  
     }  
     
     printf("The doubly linked list is ");  
     display_nodes(head);  
     printf("The doubly linked list in reverse is ");  
     display_nodes_reverse(tail);  
 }
 

Insert a node after a given node

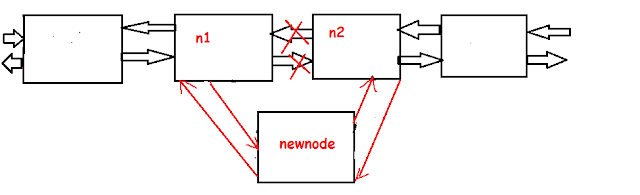
We should also be able to add the node after any given node. Or insert the node before a given node. 

Let us look back at our diagram where we are adding a new node after n1.

 As can be seen from the diagram, we should insert the new node after n1. If n2 was the node next to n1, even this n2 should be linked to n1. 

The steps needed are
  1. n2 = n1->next i.e. get the node after n1
  2. n1->next = newnode
  3. newnode->prev = n1
  4. newnode->next = n2
  5. n2->prev = newnode
The special considerations as usual is when n1 is the last node in the list. In that case n2 will be null. Hence step 5 will give segmentation fault. So 5 should be changed to 

       5. if (n2!=NULL)   n2->prev = newnode

Another thing which should be taken care when inserting after last node is modifying the tail pointer. If we add a node after tail, this new node becomes tail. 

And also since C functions are call by value, our function should use pointer to tail. That is pointer to pointer to last node. 

Hence insert_after  function is 

 void insert_after( NODEPTR*tailptr,NODEPTR newnode,NODEPTR n1)  
 {  
     //add the node between n1 and n2  
     NODEPTR n2 = n1->next;  
     n1->next = newnode;  
     newnode->prev = n1;  
     newnode->next = n2;  
     if (n2!=NULL)//if n1 is not the last node  
     {  
      n2->prev = newnode;  
     }  
     if(n1==(*tailptr))  
     {  
       *tailptr = newnode;//adding after last node. Make newnode as tail  
     }  
 }  
 int main()  
 {  
  .......  
 insert_after( &tail,newnode,currnode);

Download the program used from here 


Labels:

Comments

Post a Comment

Popular posts from this blog

Linked list in C++

A linked list is a versatile data structure. In this structure, values are linked to one another with the help of addresses. I have written in an earlier post about how to create a linked list in C.  C++ has a library - standard template library which has list, stack, queue etc. data structures. But if you were to implement these data structures yourself in C++, how will you implement? If you just use new, delete, cout and cin, and then claim it is your c++ program, you are not conforming to OOPS concept. Remember you have to "keep it together". Keep all the functions and variables together - in a class. You have to have class called linked list in which there are methods - append, delete, display, insert, find, find_last. And there will also be a data - head. Defining node We need a structure for all these nodes. A struct can be used for this purpose, just like C. struct node { int val; struct node * next; }; Next we need to define our class. W
Post a Comment
Read more

Swap nodes of a linked list

Qn: Write a function to swap the adjacent nodes of a singly linked list.i.e. If the list has nodes as 1,2,3,4,5,6,7,8, after swapping, the list should be 2,1,4,3,6,5,8,7 Image from: https://tekmarathon.com Though the question looks simple enough, it is tricky because you don't just swap the pointers. You need to take care of links as well. So let us try to understand how to go about it. Take two adjacent nodes p1 and p2 Let prevnode be previous node of p1 Now link prevnode to p2 Link p2 to p1 Link p1 to next node of p2 So the code will be prevnode -> next = p2; p1 -> next = p2 -> next; p2 -> next = p1; But what about the start node or head? head node does not have previous node If we swap head with second node, modified head should be sent back to caller  To take care of swapping first and second nodes, we can write p1 = head; p2 = head -> next; p1 -> next = p2 -> next; p2 -> next = p1; head = p2;  Now we are read
Post a Comment
Read more

Binary tree deletion - non-recursive

In the previous post we have seen how to delete a node of a binary search tree using recursion. Today we will see how to delete a node of BST using a non-recursive function. Let us revisit the 3 scenarios here Deleting a node with no children just link the parent to NULL Deleting a node with one child link the parent to  non-null child of node to be deleted Deleting a node with both children select the successor of node to be deleted copy successor's value into this node delete the successor In order to start, we need a function to search for a node in binary search tree. Did you know that searching in  a BST is very fast, and is of the order O(logn). To search Start with root Repeat until value is found or node is NULL If the search value is greater than node branch to right If the search value is lesser than node branch to left.  Here is the function NODEPTR find_node (NODEPTR root,NODEPTR * parent, int delval) { NODEPTR nd = root; NODEPTR pa = root; if (root -> v
Post a Comment
Read more